P versus NP continua sem solução comprovada

Provavelmente o maior problema conceitual em aberto da Ciência da Computação é chamado P versus NP, uma questão estudada na teoria da complexidade computacional, que lida com a proporção de recursos consumidos para se solucionar um problema computacional. Os principais recursos considerados são tempo (quantos passos são necessários) e espaço (quantidade de memória utilizada).

Conceituação

Segundo a teoria, a classe dos problemas computacionais P são aqueles que podem ser resolvidos em “tempo polinomial”. Isso significa que um computador (formalmente, uma máquina computacional sequencial e determinística) pode resolver o problema em um montante de tempo que tem proporção polinomial em relação ao tamanho da entrada do problema. Por exemplo, se para resolver um problema com n variáveis fornecidas (entrada), um computador gasta um tempo proporcional a n², ele é da classe P (uma proporção quadrática é um polinômio de grau 2).

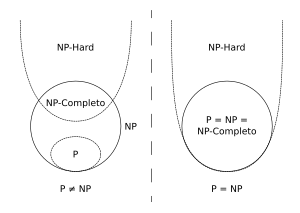
Já os problemas computacionais da classe NP (tempo não-determinístico polinomial) consistem naqueles em que uma solução conhecida pode ser verificada em tempo polinomial.

Os problemas da classe P estão contidos na classe NP, ou seja, todo problema solucionável em tempo polinomial determinístico pode ter a solução verificada também em tempo polinomial. Mas existem problemas NP difíceis, para os quais ainda não se conhece uma solução polinomial, formando a classe chamada NP-completo.

A grande dúvida da computação é se P é ou não igual a NP, ou explicando em palavras mais simples, se existem problemas que não possam ser resolvidos em tempo polinomial.

Colocando a coisa em termos mais leigos, para quem “está viajando” sem entender nada até agora. Os problemas classe P são aqueles que se pode resolver em um tempo “factível” (polinomial), enquanto os NP-completo são aqueles problemas muito difíceis, que provavelmente “demorariam demais” para serem resolvidos por um computador, embora se uma solução for previamente conhecida para um problema NP, é fácil verificá-la.

A dúvida P =? NP então seria: Os problemas NP ainda não resolvidos em tempo factível (NP-completo) são porque não há realmente uma forma polinomial de serem resolvidos (P ≠ NP), ou porque essa solução apenas ainda não foi descoberta (P = NP)?

Um exemplo prático: Considere a fatoração de um número que é produto de dois inteiros primos. Se alguém lhe disser que o número 13.717.421 pode ser escrito como o produto de dois outros inteiros, você provavelmente demorará uma imensidão de tempo para encontrar tais inteiros, pois não resta outra alternativa senão tentar fatorar (divisão inteira resto zero) o número dado por cada número primo possível. Contudo, se lhe disserem que ele é o produto de 3.607 por 3.803, você seria capaz de muito rapidamente verificar tal fato, simplesmente realizando a multiplicação e comparando o produto resultante. Fatoração de um produto de números primos é um problema NP.

Em busca da solução

O problema P versus NP é tão importante que foi definido como um dos Problemas do Milênio, sete dos mais difíceis enigmas da matemática, para os quais o Clay Mathematics Institute, em Cambridge, Massachusetts, EUA, instituiu no ano 2000 o prêmio de $1 milhão de dólares para a solução de cada um deles.

Em 11 de agosto de 2010, Vinay Deolalikar, dos Laboratórios de Pesquisa da HP em Palo Alto, EUA publicou um artigo alegando comprovar que P ≠ NP (também disponível em Scribd).

Contudo, diversos cientistas e estudiosos do assunto, como o professor Richard Lipton, do Instituto de Tecnologia da Geórgia, EUA, questionam o artigo e apontam falhas na demonstração da prova.

A comunidade científica mundial realmente suspeita que P não seja igual a NP, como buscou demonstrar Deolalikar, mas até que se comprove isso de forma inequívoca e amplamente aceita, a questão oficialmente continua em aberto.

A resposta para esse dilema não é mera questão de curiosidade científica. Muitas áreas de tecnologia envolvem problemas NP. Para citar algo crítico, modernas técnicas de criptografia digital tem sua segurança baseada na dificuldade de problemas NP-completo. Se alguém por acaso conseguir provar o contrário do que propõe Deolalikar, ou seja, que P = NP, implicaria afirmar que teoricamente existiriam meios de se desfazer a segurança da moderna criptografia em tempo polinomial.

Para saber mais:

• Solução para maior problema da computação está provavelmente errada, 2010-08-13, da NEW SCIENTIST, em Folha.com.
• Resolvido o duelo entre P e NP?, por Carlos Orsi, 2010-08-09, em Estadão Blogs – A ciência na sua vida: Matemática.
• Tide turns against million-dollar maths proof (em inglês), por Jacob Aron, 2010-08-13, New Scientist.
• Verbetes relacionados na Wikipédia em Português: P versus NP; NP (complexidade); NP-difícil; NP-completo.
• Verbete na Wikipedia em Inglês: P versus NP problem; P (complexity); NP (complexity); Time complexity – Polynomial time; NP-hard; NP-complete.
• Complexity Zoo (em inglês).